The Wave Kernel Signature: A Quantum Mechanical Approach To Shape Analysis
IEEE International Conference on Computer Vision (ICCV) - Workshop on Dynamic Shape Capture and Analysis (4DMOD), 2011
Wave Kernel Signature
Mathieu Aubry, Ulrich Schlickewei, Daniel Cremers
Abstract
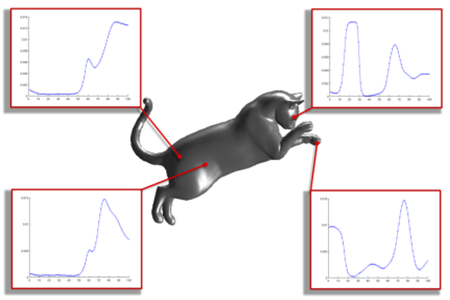
The Wave Kernel Signature characterize each point of a 3D shape.
Each value of the WKS can be intepreted in the framework of quantum mechanic as the average probability to find a particle of a given energy at a given point.
Mathematicaly, the WKS is based on the eigen-functions and eigen-values of the Laplace-Beltrami operator on the shape
It provides an optimal combination of the eigen-functions values to construct a disciminative and robust descriptor.
Code
You can download a matlab function which compute the WKS of all points of a shape given a set of vertices and faces here
Related Publications
Pose-Consistent 3D Shape Segmentation Based on a Quantum Mechanical Feature Descriptor
Pattern Recognition (Proc. DAGM), Springer, 2011
News
If you are interested in spectral methods in shape amalysis, look at our NORDIA 2014 paper on Anisotropic Laplace-Beltrami Operators for Shape Analysis .Copyright Notice
The documents contained in these directories are included by the contributing authors as a means to ensure timely dissemination of scholarly and technical work on a non-commercial basis. Copyright and all rights therein are maintained by the authors or by other copyright holders, notwithstanding that they have offered their works here electronically. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright.