Generative Escher Meshes

This paper proposes a fully-automatic, text-guided generative method for producing periodic, repeating, tile-able 2D art, such as the one seen on floors, mosaics, ceramics, and the work of M.C. Escher.

In contrast to the standard concept of a seamless texture, i.e., square images that are seamless when tiled, our method generates non-square tilings which comprise solely of repeating copies of the same object. It achieves this by optimizing both geometry and color of a 2D mesh, in order to generate a non-square tile in the shape and appearance of the desired object, with close to no additional background details.

We enable geometric optimization of tilings by our key technical contribution: an unconstrained, differentiable parameterization of the space of all possible tileable shapes for a given symmetry group. Namely, we prove that modifying the laplacian used in a 2D mesh-mapping technique - Orbifold Tutte Embedding - can achieve all possible tiling configurations for a chosen planar symmetry group. We thus consider both the mesh's tile-shape and its texture as optimizable parameters, rendering the textured mesh via a differentiable renderer. We leverage a trained image diffusion model to define a loss on the resulting image, thereby updating the mesh's parameters based on its appearance matching the text prompt.

We show our method is able to produce plausible, appealing results, with non-trivial tiles, for a variety of different periodic tiling patterns.

What do we call a tileable shape?

We say a shape is tileable with regards to a symmetry group if the action of the group on the shape creates a tessalation of the plane, i.e. a covering with no gaps, nor overlaps. There exist only 17 such symmetry groups, called the wallpaper groups.

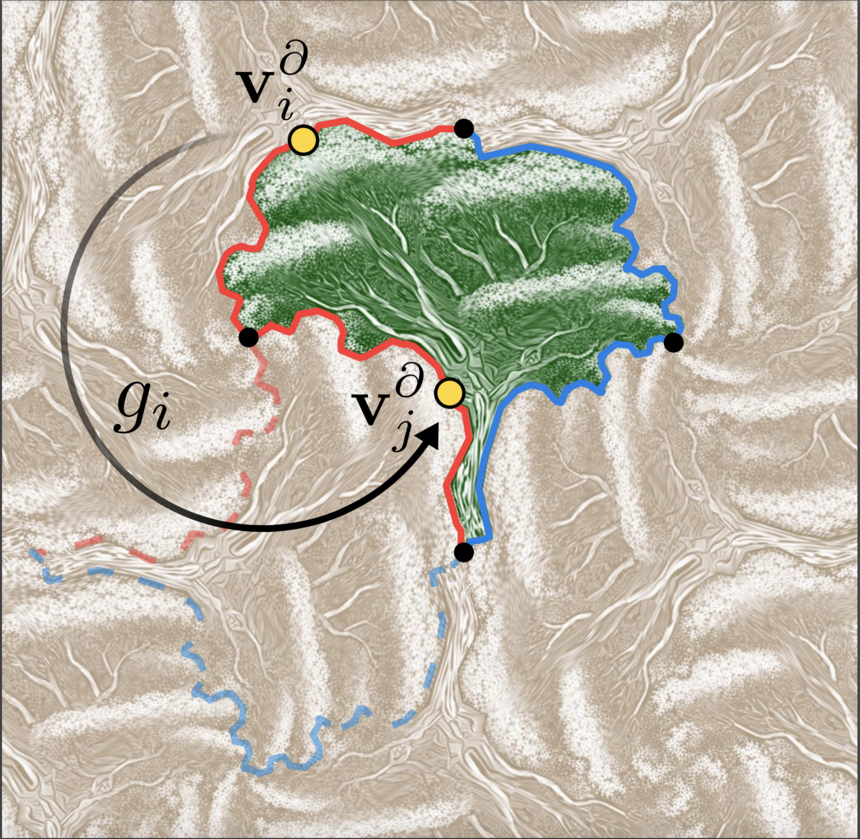
The tiling's basic structure. The tile (in green) is mapped to a copy of itself (dashed boundary) by an isometry g_i which is a member of the wallpaper group describing the symmetries of the desired tiling. The boundary vertex v_i^∂ is mapped by g_i exactly to another boundary vertex, v_j^∂. This results in a correspondence along the boundary, visualized via matching boundary colors - one for each of the two symmetries which generate the tiling. Black vertices are fixed axes of rotation.

Overview

Overview of our method. We optimize the weights W and the texture image \(\mathcal{I}\). The edge weights W are used to construct the Laplacian used in the linear system of OTE~[Aigerman 2015]. The solution of this linear system assigns new positions V to the vertices of the mesh, which is guaranteed to represent a valid tile, with no self-overlaps, that can tile the plane perfectly - because those constraints translate to equations in the linear system. The mesh is textured using the texture image \(\mathcal{I}\) and rendered via a differentiable renderer, producing the final rendered image \(\mathcal{R}\) of the textured tile, which is then input into Score Distillation Sampling~[Poole 2022], from which gradients are back-propagated to the optimizable parameters - W and \(\mathcal{I}\), which control the shape and texture of the tile.

Multi-tile generation. Our approach can optimize simultaneously for two tile shapes for two different prompts, by having each shape consist of half of the underlying mesh. The same can be achieved for more than two sub-parts.

During optimization, we visualize the mesh, and the resulting tiling. The gradients provided by the visual loss, Score Distillation Sampling, are very noisy and vary wildly in magnitude. Because of our injectivity constraints and periodic constraints, the shape we optimize is garanteed to remain always tileable.

We can 3D print the generated tiles! We print the "Flamenco Dancer". via the website Shapeways, using four different color. On the right, we show the beginning of the plane tessellation using this tiles. This showcases the possibility of physically creating tiles that are unique in the world, and using them for decoration and design.

[Kaplan 2000] Craig S. Kaplan and David H. Salesin. 2000. Escherization. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH '00). Escherization is a major inspiration of this work, creating Escher-like tilings by fitting an n-gon to an image.

[Aigerman 2015] Noam Aigerman and Yaron Lipman. 2015. Orbifold tutte embeddings. ACM Trans. Graph. Key reference showing how to create an injective map from 2D patch to another respecting periodic constraints.

BibTeX

@article{escher2023,
  author    = {Noam Aigerman and Thibault Groueix},
  title     = {Generative Escher Meshes},
  journal   = {SIGGRAPH},
  year      = {2024},
}

Generative Escher Meshes