Abstract

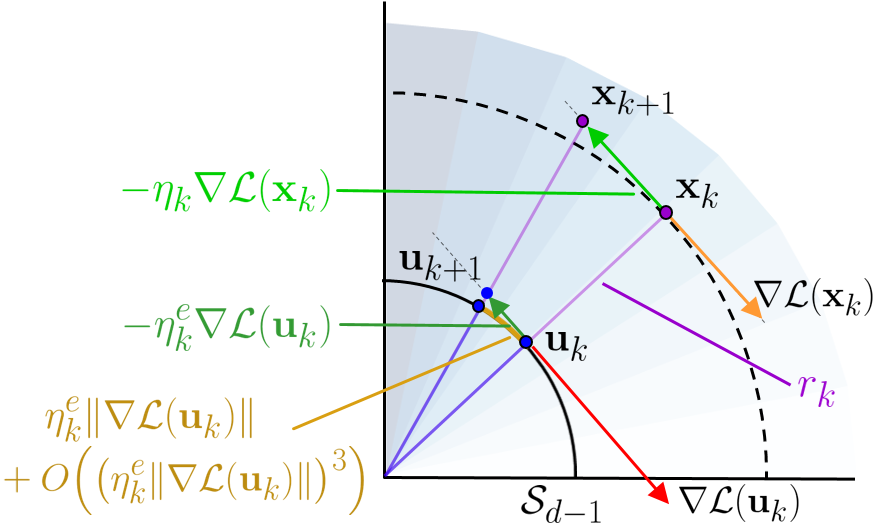
Batch Normalization (BN) is a prominent deep learning technique. In spite of its apparent simplicity, its implications over optimization are yet to be fully understood. In this paper, we study the optimization of neural networks with BN layers from a geometric perspective. We leverage the radial invariance of groups of parameters, such as neurons for multi-layer perceptrons or filters for convolutional neural networks, and translate several popular optimization schemes on the $L_2$ unit hypersphere. This formulation and the associated geometric interpretation sheds new light on the training dynamics and the relation between different optimization schemes. In particular, we use it to derive the effective learning rate of Adam and stochastic gradient descent (SGD) with momentum, and we show that in the presence of BN layers, performing SGD alone is actually equivalent to a variant of Adam constrained to the unit hypersphere. Our analysis also leads us to introduce new variants of Adam. We empirically show, over a variety of datasets and architectures, that they improve accuracy in classification tasks.

Paper and Code

To cite our paper,

@INPROCEEDINGS{roburinspherical2020,
    author    = {Simon Roburin and Yann de Mont-Marin and Andrei Bursuc and Renaud Marlet and Patrick Perez and Mathieu Aubry},
    title     = {Spherical Perspective on Learning with Batch Norm},
    booktitle = {Arxiv},
    year      = {2020}}